Welcome back to our fourth article on GMAT circles. Last time we considered inscribed angles and learned that where there is a 90-degree inscribed angle, there is a hypotenuse that is also a diameter of the circle. This time we will explore a class of problems where the radius, rather than the diameter, pulls double duty as a hypotenuse. Let’s dive right in with the following official problem.
1. Radius as Hypotenuse – GMAT Official Problem
The figure above represents a semicircular archway over a flat street. The semicircle has a center at O and a radius of 6 feet. What is the height h, in feet, of the archway 2 feet from its center?
A. √2
B. 2
C. 3
D. 4√2
E. 6
This problem is a straightforward application of the Pythagorean theorem. Since we are told that the radius of the semicircle is 6 feet, we can draw a 6-foot radius from center O to the point where height h meets the semicircle. Voila – a right triangle.
h = √(62 – 22)
h = √(36 – 4)
h = √32
This is where you should stop and mark answer choice D since we are taking the square root of a number that is not a perfect square. When we simplify this radical, something will get left inside. Therefore answers B, C, and E are out (Answer A is out because √2 =/= √32), and the correct choice is D.
2. Radius as Hypotenuse Problem 1
Let’s try something a little different:
In the xy-plane, point (r,s) lies on a circle with center at the origin. What is the value of r² + s²?
1. The circle has radius 2.
2. The point (2,-2) lies on the circle.
A. Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B. Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D. EACH statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
This is the first problem we’ve seen where a circle is placed on the xy-plane. In such problems, it is usually helpful to remember the basic circle principle that every point on the circle (meaning on its edge or perimeter) is equidistant from its center.
Solution
If you’re unfamiliar with these problems, statement 1 may trip you up. Is the radius of the circle sufficient to determine r² + s²? Yes, it is. If you are concerned about the unknown positivity/negativity of the coordinates r and s, recall that the square of any number (except 0) is positive. This means that for any positive/negative combination of r and s, the sum r² + s² will have the same value.
But what you really need here is to see that the expression r² + s² matches the famous a² + b² from the Pythagorean theorem, and in fact, it functions the exact same way.
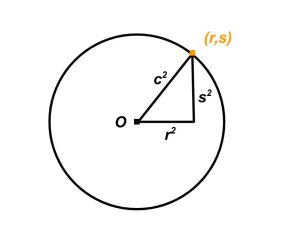In this setup, the radius is the hypotenuse of the right triangle with legs r and s. Therefore, applying the Pythagorean theorem, the value r² + s² represents the square of the radius. So if we know the value of the radius (2), we know the value r² + s², and statement 1 is sufficient.
Statement 2 offers that the point (√2, -√2) lies on the circle. This statement should be “easier” to evaluate than statement 1. Seeing the radicals in the coordinates ought to help you make the connection to the Pythagorean theorem if you didn’t already while evaluating statement 1. But using the principle that every point on a circle is equidistant from its center, we know that this given point (√2, -√2) is the same distance from the center as the point (r, s) in the question. Therefore if we sum the squares of √2 and -√2, the result (4) will also represent the value r² + s² we were asked about.
3. Problem 2
Let’s try one more:
In cross section, a tunnel that carries one lane of one-way traffic is a semicircle with radius 4.2 m. Is the tunnel large enough to accommodate the truck that is approaching the entrance to the tunnel?
1. The maximum width of the truck is 2.4 m.
2. The maximum height of the truck is 4 m.
A. Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B. Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D. EACH statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
This one is a little more complex. Sometimes on GMAT quant problems, it is helpful to ask why certain details were specified. In this case, we are told that the tunnel “carries one lane of one-way traffic.” This is important because if it were not the case, the truck would have to drive on one side or the other, and there’s no way it would be able to get through the tunnel. Since there is only one lane going through the tunnel, the truck can “center up” to give itself the best chance of fitting through.
Solution
This is one of those less-common DS problems where each statement on its own is clearly insufficient. If all we know is that the truck is 2.4m wide at its widest point (statement 1), it may still be too tall to fit through the tunnel. If all we know is that the truck is 4m tall at its tallest point, we don’t know whether the truck is narrow enough to make it through the tunnel while being this tall.
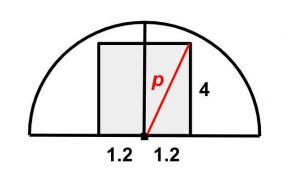But if we combine statements 1 and 2, we can use the Pythagorean theorem to calculate the max distance of a point on the “centered up” truck from the point at the “center” of the semicircle.
Now here’s the key step: don’t calculate! Running the Pythagorean theorem with our values here would be a waste of time. As long as the value p [from the graphic] is less than 4.2 (the radius of the tunnel), the truck will fit. But for DS, we don’t have to know whether the truck will fit. All we have to know is whether the value p can be calculated, and in this case, it can be. Statements 1 and 2 together are sufficient, and the correct answer choice is C.
This concludes our fourth article on the GMAT’s treatment of circles. Next time we will look at circles in two different 3-dimensional shapes: cylinders and spheres.
Contributor: Elijah Mize (Apex GMAT Instructor)