GMAT Triangles
Close your eyes, imagine a triangle, then open your eyes again.
Which of the following did you picture? Something different?
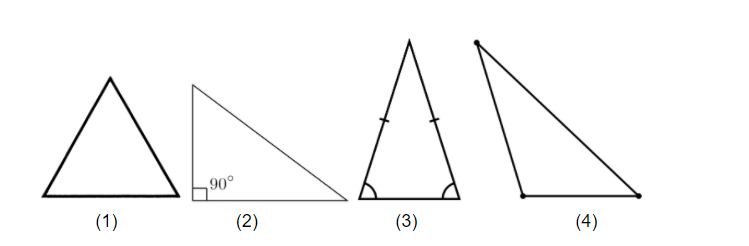
Well, every one of the above is tested on the GMAT. And you can’t stick to just one conception of a single shape. You have to be familiar with different types of triangles and all of their characteristics.
For example, suppose you need to find the two-dimensional area within a triangle. What’s the proper way to do this for a right triangle (2), which contains a 90-degree angle? Even if I know the proper formula, would applying it prove different if I needed to use it on triangle (4), an obtuse triangle, which has one angle greater than 90 degrees?
What about the perimeter, or the sum of the lengths of the three sides of the triangle? Are there simple, straightforward ways to calculate this in the case of the equilateral triangle (1), where each side is the same length. Or the isosceles triangle (3), where two of the three sides are the same length?
What about that isosceles triangle? Did you notice that the two sides that are the same length are opposite two angles of equal measure? What are the implications of this?
How about the fact that all the angles in any triangle add up to the same degree measure, no matter how the triangle looks?
And then there’s something as simple as the base of the triangle. Take triangle (4):
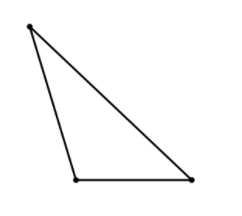
As shown, the shortest side is the base, or bottom side, of the triangle. But in truth, any side of a triangle could be considered the base. What if we took the same triangle and rotated it clockwise:
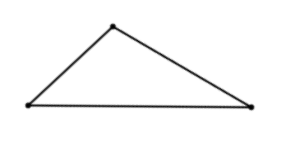 Now suddenly, the same triangle has the longest side as its base. This could completely change how you calculate, for example, the area of the triangle.
Now suddenly, the same triangle has the longest side as its base. This could completely change how you calculate, for example, the area of the triangle.
What about the relationships among the sides of a right triangle, for example?

It turns out that the sides a, b, and c, of all right triangles conform to a special mathematical relationship, no matter their lengths. And in its most elementary forms as well. For example, did you know that if a right triangle has short sides (legs) of lengths 3 and 4, the longest side (hypotenuse) will always be 5?
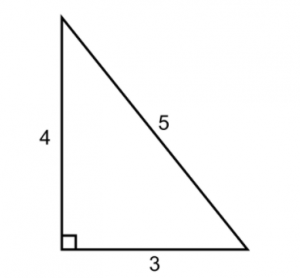
The GMAT is less interested in very complex math and much more interested in variations on basic facts like this one.
Also, what happens when triangle types are combined? What happens when a triangle is both isosceles AND right? How does this affect the relationships among the sides?
Another way the test can give triangles (and other shapes) a twist is to combine them with other shapes. You may see questions that involve, for example, a triangle within a circles (inscribed):
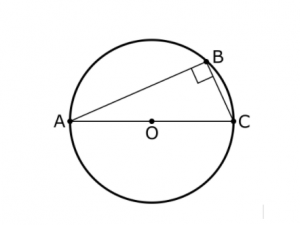 This presents all sorts of opportunities for testing not only the measurements of triangles and of circles individually but also the relationships among those measurements and the ways in which they might overlap.
This presents all sorts of opportunities for testing not only the measurements of triangles and of circles individually but also the relationships among those measurements and the ways in which they might overlap.
This is of course meant to be a brief overview of the basic forms GMAT triangles can take. But the above poses critical thinking questions you should examine as you move forward with your preparation. Remember: don’t just think in terms of memorizing facts! There will be a handful of formulas to know, to be sure, but once those are out of the way, it will be up to you to be on the lookout for new ways that knowledge could be applied and tested.
As the next step in your discovery and practice of GMAT triangles visit these posts:
A Short Meditation on Triangles
The 30-60-90 Right Triangle
The 45-45-90 Right Triangle
The Area of an Equilateral Triangle
Triangles with Other Shapes
Isosceles Triangles and Data Sufficiency
Similar Triangles
3-4-5 Right Triangle
5-12-13 and 7-24-25 Right Triangles
Triangle Inequality Rule
By: Rich Zwelling, Apex GMAT Instructor
Date: 15th December, 2020
