Last time, we looked at the following GMAT combinatorics practice problem, which gives itself away as a PERMUTATION problem because it’s concerned with “orderings,” and thus we care about the order in which items appear:
At a cheese tasting, a chef is to present some of his best creations to the event’s head judge. Due to the event’s very bizarre restrictions, he must present exactly three or four cheeses. He has brought his best cheddar, brie, gouda, roquefort, gruyere, and camembert. How many potential orderings of cheeses can the chef create to present to the judge?
A) 120
B) 240
C) 360
D) 480
E) 600
(Review the previous post if you’d like an explanation of the answer.)
Now, let’s see how a slight frame change switches this to a COMBINATION problem:
At a farmers market, a chef is to sell some of his best cheeses. Due to the market’s very bizarre restrictions, he can sell exactly two or three cheeses. He has brought his best cheddar, brie, gouda, roquefort, gruyere, and camembert. How many potential groupings of cheeses can he create for display to customers?
A) 6
B) 15
C) 20
D) 35
E) 120
Did you catch why this is a COMBINATION problem instead of a PERMUTATION problem? The problem asked about “groupings.” This implies that we care only about the items involved, not the sequence in which they appear. Cheddar followed by brie followed by gouda is not considered distinct from brie followed by gouda followed by cheddar, because the same three cheeses are involved, thus producing the same grouping.
So how does the math work? Well, it turns out there’s a quick combinatorics formula you can use, and it looks like this:
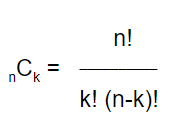
Let’s demystify it. The left side is simply notational, with the ‘C’ standing for “combination.” The ‘n’ and the ‘k’ indicate larger and smaller groups, respectively. So if I have a group of 10 paintings, and I want to know how many groups of 4 I can create, that would mean n=10 and k=4. Notationally, that would look like this:
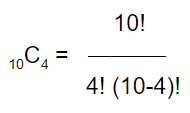
Now remember, the exclamation point indicates a factorial. As a simple example, 4! = 4*3*2*1. You simply multiply every positive integer from the one given with the factorial down to one.
So, how does this work for our problem? Let’s take a look:
At a farmers market, a chef is to sell some of his best cheeses. Due to the market’s very bizarre restrictions, he can sell exactly two or three cheeses. He has brought his best cheddar, brie, gouda, roquefort, gruyere, and camembert. How many potential groupings of cheeses can he create for display to customers?
A) 6
B) 15
C) 20
D) 35
E) 120
The process of considering the two cases independently will remain the same. It cannot be both two and three cheeses. So let’s examine the two-cheese case first. There are six cheese to choose from, and we are choosing a subgroup of two. That means n=6 and k=2:
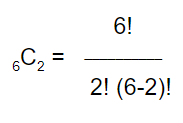
Now, let’s actually dig in and do the math:
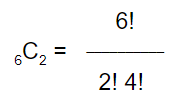
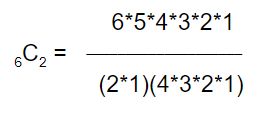
From here, you’ll notice that 4*3*2*1 cancels from top and bottom, leaving you with 6*5 = 30 in the numerator and 2*1 in the denominator:
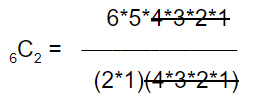 That leaves us with:
That leaves us with:
6C2 = 15 combinations of two cheeses
Now, how about the three-cheese case? Similarly, there are six cheeses to choose from, but now we are choosing a subgroup of three. That means n=6 and k=3:
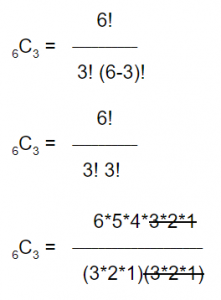
From here, you’ll notice that the 3*2*1 in the bottom cancels with the 6 in the top, leaving you with 5*4 = 20 in the numerator:
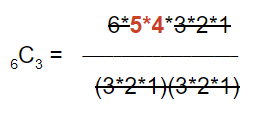
That leaves us with:
6C3 = 20 combinations of three cheeses
With 15 cases in the first situation and 20 in the second, the total is 35 cases, and our final answer is D.
Next time, we’ll talk about what happens when we have permutations with repeat elements.
In the meantime, as an exercise, scroll back up and return to the 10-painting problem I presented earlier and see if you can find the answer. Bonus question: redo the problem with a subgroup of 6 paintings instead of 4 paintings. Try to anticipate: do you imagine we’ll have more combinations in this new case or fewer?
Permutations and Combinations Intro
A Continuation of Permutation Math
An Intro To Combination Math
Permutations With Repeat Elements
Permutations With Restrictions
Combinations with Restrictions
Independent vs Dependent Probability
GMAT Probability Math – The Undesired Approach
GMAT Probability Meets Combinatorics: One Problem, Two Approaches
By: Rich Zwelling, Apex GMAT Instructor
Date: 23rd February, 2021
