By: Rich Zwelling, Apex GMAT Instructor
Date: 7th January, 2021
30-60-90 Right Triangle
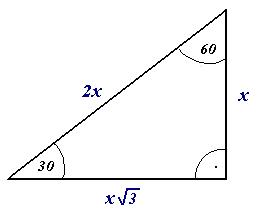
In a previous piece, we covered the 45-45-90 right triangle, also known as the isosceles right triangle. There is another so-called “special right triangle” commonly tested on the GMAT, namely the 30-60-90 right triangle.
Like the isosceles right, its sides always fit a specific ratio, as seen in the above diagram (1 : √3 : 2). And it’s worth noting, as with all triangles, that the shortest side is opposite the smallest angle, while the longest side is opposite the largest angle, etc.
Now, it’s easy enough to memorize this ratio and deduce what each side length will be, given that we are dealing with a 30-60-90 triangle. For example, Suppose we are given the following information:
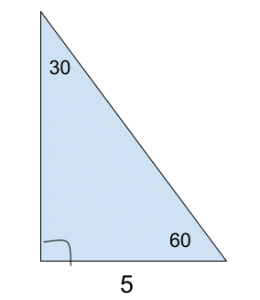
This is low-level memorization, and we can deduce that the side opposite the 60-degree angle will be length 5√3, while the hypotenuse will be length 10.
But let’s look to this GMAT Official Guide problem to see something a little more high-level. Give it a shot before reading further:
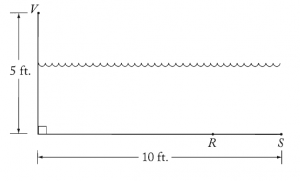
In the figure above, V represents an observation point at one end of a pool. From V, an object that is actually located on the bottom of the pool at point R appears to be at point S. If VR = 10 feet, what is the distance RS, in feet, between the actual position and the perceived position of the object?
(A) 10−5√3
(B) 10−5√2
(C) 2
(D) 2 1/2
(E) 4
(For starters, notice that the question they’re asking for — the distance between the actual position and the perceived position — is just line segment RS. Remember that the GMAT is very good at using complicated wording to frame a simple concept. Always simplify the question as quickly as possible.)
To understand this problem, let’s first talk about one of the higher-level ways the GMAT could test 30-60-90 triangles. Take this example:
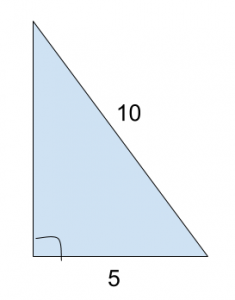Notice we are given no angles except the right angle. But we do have 2 sides and 1 angle in total, which is sufficient to form a unique triangle. Furthermore, did you identify anything that gives this away as a 30-60-90?
The hypotenuse is twice the length of one of the sides, giving them a 2:1 ratio. That guarantees that the third side fits the √3 component of our ratio, giving that side a length of 5√3. So even without labeled angles:
A right triangle with a hypotenuse twice the length of one of its legs must be a 30-60-90 triangle.
That’s much more the kind of critical thinking the GMAT is interested in testing.
Similarly, in this Official Guide problem, we are told that VR is length 10:
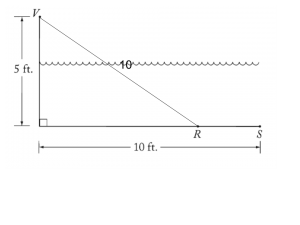
Notice that at this point, it’s up to you to make the deduction that we have a 30-60-90 triangle, and thus the distance from the right angle marker to point R must be 5√3:
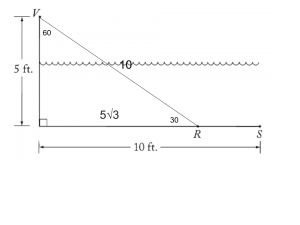
From there, it’s straightforward to see that RS is simply the marked length of 10 minus the length of 5√3 we just deduced, thus leading us to answer choice A.
In terms of strategy, another point: a brief look at the answer choices at the start of the problem gives a strong hint that either a 30-60-90 or 45-45-90 triangle is involved. Notice that the first two answers feature a √3 and a √2 term, and this is clearly a geometry question. This gives you the opportunity to be preemptive and use the test’s patterns against itself.
It goes without saying that these kinds of problems get easier to be solved with practice. Solve as many problems as you can, compare and contrast the strategies you used, and make sure you understand the process properly. You can also consider having a GMAT tutor to help you during your GMAT prep and get a stellar score.
In our next post, we’ll talk about how 30-60-90 triangles can be used directly to calculate the area of equilateral triangles. You can also link to our other article about triangles:
A Short Meditation on Triangles
The 30-60-90 Right Triangle
The 45-45-90 Right Triangle
The Area of an Equilateral Triangle
Triangles with Other Shapes
Isosceles Triangles and Data Sufficiency
Similar Triangles
3-4-5 Right Triangle
5-12-13 and 7-24-25 Right Triangles